Lab 2: CMOS Adder
When entering numeric values in the answer fields, you can use integers (1000, 0x3E8, 0b1111101000), floating-point numbers (1000.0), scientific notation (1e3), engineering scale factors (1K), or numeric expressions (3*300 + 100).
Useful links:
Problem 1. CMOS basics
The following questions are multiple-choice. You can, of course, simply keep guessing until you get the right answer. But youʼll be in a much better position to take the quizzes if you take the time to actually figure out the answers.
- If we set the inputs of a particular CMOS gate to voltages that correspond to valid logic levels, we would expect the static power dissipation of the gate to be
- Measuring a particular CMOS device G, we find 1.5V noise margins. If the width of all mosfets inside of G were doubled, we would expect the noise margins of the new gate to
- To decrease the output rise time of a CMOS gate one could
- The Boolean function F(A,B,C,D) of four inputs is implemented as a single CMOS gate whose output connects to a pullup circuit containing only PFETs and a pulldown containing only NFETs. The output of F is known to depend on its inputs; i.e., F(A,B,C,D) is zero for certain input combinations and one for others. What can you deduce about F(1,1,1,1)?
Problem 2. Power dissipation
Almost all of the power dissipated by CMOS circuits goes into charging and discharging nodal capacitances. This power can be computed as \(CV^2F\) where \(C\) is the capacitance being switched, \(V\) is the change in voltage, and \(F\) is the frequency at which the switching happens. In CMOS circuits, nodes are switched between ground (0 volts) and the power supply voltage (\(V_{DD}\) volts), so \(V\) is either +\(V_{DD}\) (for a 0→1 output transition) or \(-V_{DD}\) (for a 1→0 output transition) and so \(V^2 = V_{DD}^2\).
Problem 3. CMOS logic gates
As we saw in lecture, there are 16 possible 2-input combinational logic gates. The cost of implementing these gates varies dramatically, requiring somewhere between 0 and 10 mosfets depending on the gate. For example, it takes 2 mosfets to implement "F = NOT A", but 4 mosfets (organized as two inverters) to implement "F = A".
For each of the 2-input gates whose Karnaugh maps are given below, indicate the minimum number of mosfets required to implement the gate. You should only consider static fully-complementary circuits like those shown in lecture; these implementations meet the following criteria:
- no static power dissipation
- \(V_{OL} = 0V\), \(V_{OH}\) = power supply voltage
- NFETs appear only in pulldown circuits, PFETs appear only in pullup circuits
- the pullup and pulldown are complementary, i.e., when one path is "on", the other is "off"
- the pullup and pulldown circuits can be decomposed into series and parallel connections of mosfets
- all gate implementations restore incoming logic levels (so a wire connecting an input terminal to an output terminal would not be a legal gate implementation)
-
-
-
Hint: see the Design Problem below.
-
-
Problem 4. Design Problem: 3-bit adder
Your mission is to design and test a CMOS circuit that performs addition of two twoʼs-complement 3-bit numbers, producing a 4-bit result:
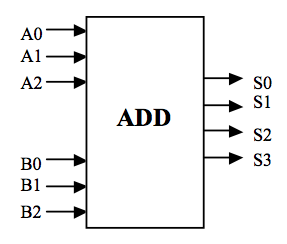
Ripple-carry adders
Letʼs start with a simple ripple-carry adder based on the full-adder module, which has 3 inputs (\(A\), \(B\) and \(C_{IN}\)) and 2 outputs (\(S\) and \(C_{OUT}\)). The full adder computes the sum of \(A\), \(B\) and \(C_{IN}\) and outputs the 2-bit answer on \(C_{OUT}\) and \(S\). The logic equations and truth table for \(S\) and \(C_{OUT}\) are shown below.
$$S = A \oplus B \oplus C_{IN} \qquad C_{OUT}=A\cdot B + A\cdot C_{IN} + B\cdot C_{IN}$$| \(A\) | \(B\) | \(C_{IN}\) | \(S\) | \(C_{OUT}\) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
A ripple-carry adder is simply a chain of full adder modules that compute the sum bit-by-bit, like so:
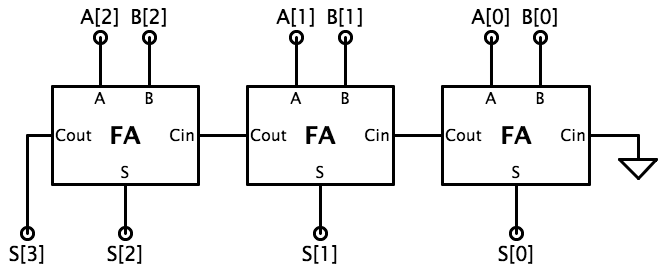
There are three goals for your implementation. First, of course, is computing the right outputs. The other two goals involve some engineering tradeoffs: small circuit size, as measured by the total number of mosfets, and fast performance, as measured by the \(t_{PD}\) of the ADDER3 circuit. In ripple-carry adders, the longest path is through the carry chain that connects the full adder (FA) modules, i.e., through the \(C_{IN}\) to \(C_{OUT}\) path of each FA module in turn. So try to minimize the \(t_{PD}\) of the logic that computes \(C_{OUT}\).
Typically \(S\) is implemented using two cascaded 2-input XOR gates. You can use ANDs and ORs in a sum-of-products implementation for \(C_{out}\), but for speed think about using three 2-input NANDs and one 3-input NAND to implement \(C_{out}\) (remember that by Demorganʼs Law two cascaded NANDs are logically equivalent to a cascade of AND/OR).
Build your own gate library
Since weʼre using individual gates to implement the logic, a good place to start is to build your own gate library (e.g., inverter, 2-input NAND, 2-input XOR, ...), test them individually, and then use them to implement your design. Itʼs much easier to debug your circuit module-by-module rather than as one big lump. XOR can be a challenging gate to design; hereʼs one suggestion for how it might be implemented based on the observation that \(\textrm{XOR}(A,B)\) is true when \(A\) and \(B\) are not \(11\) or \(00\):
$$\textrm{XOR}(A,B) = \overline{A\cdot B + \overline{A}\cdot\overline{B}} = \overline{A\cdot B + \overline{A + B}} = \overline{A\cdot B + \textrm{NOR}(A,B)}$$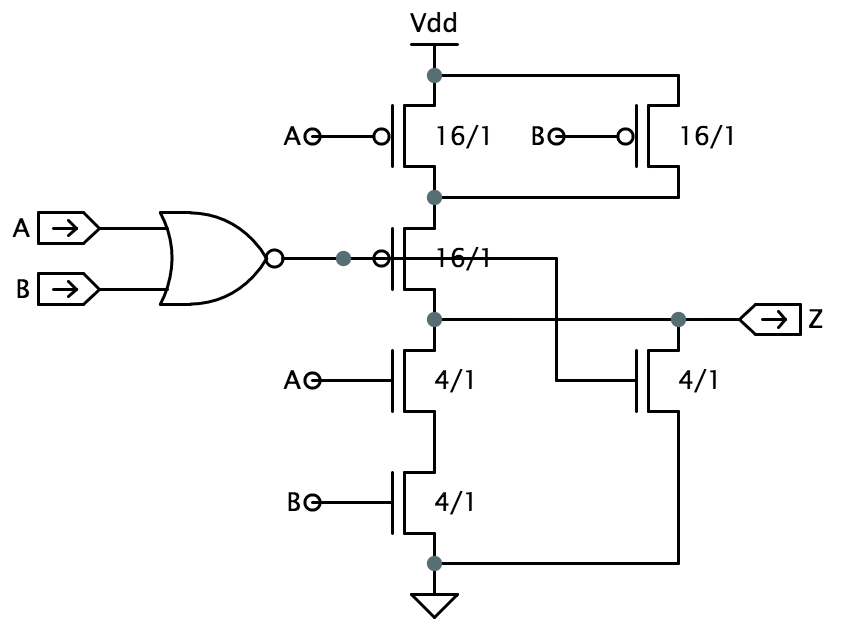
The large, black "connection dots" in the schematic show where crossing signal wires connect. In the figure above, the output of the NOR2 gate connects to the gate of the PFET then goes on to connect to the gate of the NFET at the bottom right. It crosses over but does not connect to the Z wire. The triangle symbol at the bottom is a connection to ground; the T-shaped symbol at the top is a connection to \(V_{DD}\).
Click on the button below to open the Jade instance where youʼll enter your design.
Weʼve provided skeleton modules for most of the logic gates — each module includes a schematic icon and a functional test, but youʼll need to build the schematic for any gates you use in your design. Weʼve provided schematics for the inverter and for the AND and OR gates, which are built using the corresponding NAND and NOR gates.
Suggested steps:
- Select the "/adder/fa" module using the module selection box at the top. Design the circuit youʼll use to implement the FA functionality then click and drag the gates needed from the parts bin on the right into your schematic. Arrange the gates and input/output ports tastefully, then add wires to make the appropriate connections.
- Enter a schematic for each logic gate you used in Step 1:
select
the appropriate module, then drag NFETs and PFETs from the
parts bin into the schematic to build a CMOS implementation of the
gate. You can click and drag the icons for ground and \(V_{DD}\)
from the toolbar at the top of the schematic to make connections
for the pulldowns and pullups. Remember to hook up the input/output ports.
Take a look at the /adder/inverter module to see what a finished
gate schematic looks like.
Now click the green checkmark in the toolbar in order to run the test to verify that youʼve correctly implemented the gate.
- Once all the necessary logic gates have been designed and verified, return to the /adder/fa module and verify its implementation by clicking on the green checkmark.
- After your FA implementation is correct, select the /adder/adder3 module and click the green checkmark to verify correct operation of the ADDER3 module and complete the design task. Since this is a large circuit, the simulation will take awhile — be patient! When this simulation completes successfully, the system will give you credit for completing this design problem.